NOT ALL WHO WANDER ARE LOST (ON ANDROID.COM)
The Problem: One of the most frequently visited pages on Android.com is their 404 Not Found error page. This is a natural occurrence stemming from decades of outdated links pointing to Android.com/XYZ, which don't exist anymore.
The Android team challenged us with transforming what was a navigational dead-end into a switchboard to help lost users renavigate. That main problem was addressed functionally by a convenient dropdown that allowed a user to quickly continue on to the main destinations of Android.com. No sweat!
With that solved, we had an opportunity now to do much more to give somehow give a moment of joy to millions of people, a moment which is most times forgettable at best.
So we pitched a retro-future arcade experience (hidden in the back piping of Android.com) where users help our Bugdroid friends by helping to steer these sweet bites (bytes?) to their internet destinations.
We had heaps of fun working on this and won an Awwwards Site of the Day with an 8.04 in creativity!
IS there an optimal strategy to 404?
Designing for Flow
In designing for games, tuning the balance of difficulty and user skill level is often the most time consuming and under appreciated steps that can take the experience from a casual amusement (or frustrating impossibility) to an addicting, all-consuming challenge.
We set experiential goals based on Mihaly Csikszentmihalyi's theory of Flow where a user's skill level and the experiences difficulty scale in proportion to another to maximize mental engagement. With a defined user base across the entire spectrum of ages, devices and geographic locales, we knew it would be tough to optimize this for every user with any precision. In alignment with the friendly Android brand, we decided to err on the safer side of ease and boredom for a wider audience appeal, making up for any potential lack of engagement with fun animations, sound and surprises such as bonus candies (Nougats) and unlocking a Disco Mode.
In defining a difficulty basis to tune the game to, I asked myself: Is there an optimal strategy to this game? To start somewhere, I decide to define an optimal solution as a single default state that requires the least amount of deviations to address every possible scenario. To get towards a strategy, let's define the basic components of the game.
404's Game Mechanics PrimeR
These four pieces, Donut, Jellybean, Marshmallow and Nougat can enter from the two entrance points. The entrances are located at the top left of the board, and the bottom right.
The basic premise of the game is the user gets points for matching the confectionaries entering the board to the correct goal pipe, which are pink, blue and white, respectively corresponding to the donut, jellybean and marshmallow pieces. The nougat piece can enter any goal pipe, so for the purposes of strategy they are insignificant and can be ignored.
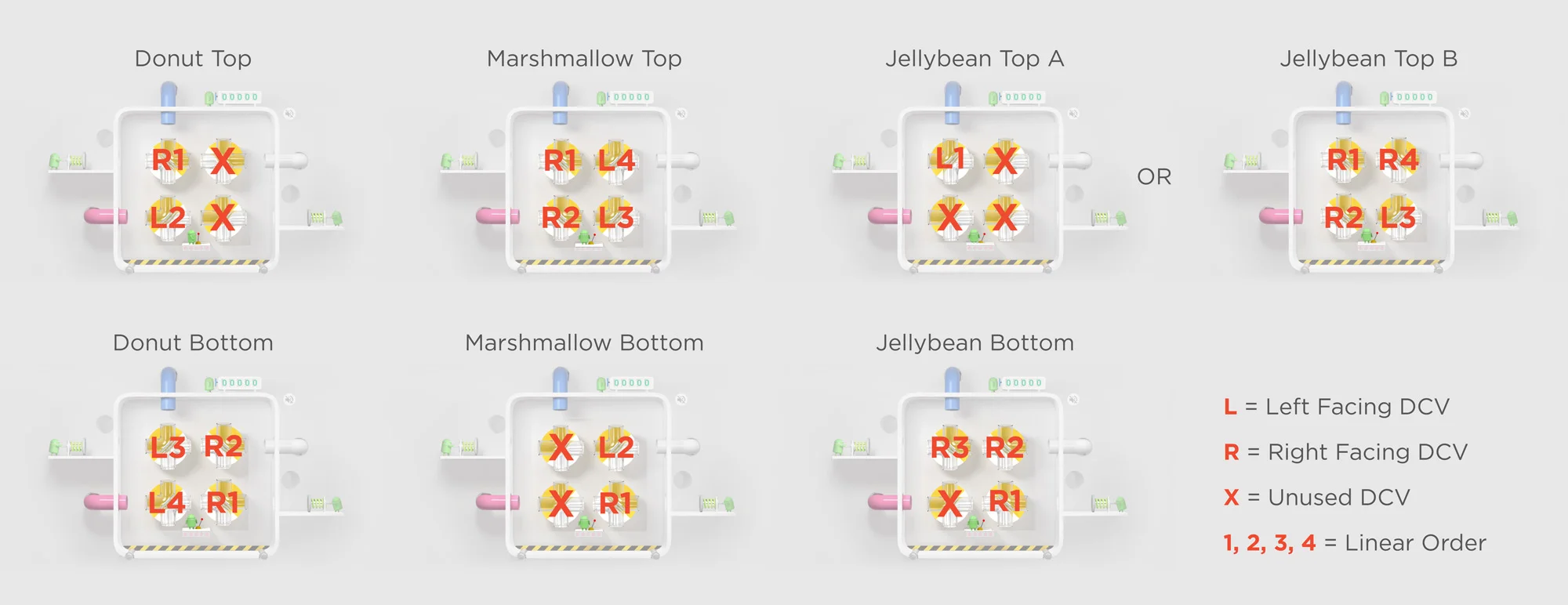
Users change the direction of the incoming pieces towards their goal pipes by interacting with the four Directional Control Valves (DCV’s) in the center area of the board. They change directions of the pieces into all four potential directions, dependent on which side the entering piece comes from. To allow for a solution analysis that is independent of the entering piece direction, we'll consider the direction of the DCV itself, of which there are only two states.
Each DCV is bi-directional. We will call it Left (L) when the yellow half is predominantly on the left hand side and Right (R) when the yellow half is predominantly on the right. Clicking the DCV will have it change between the binary states. This allows us to map each piece from the two entrance locations (Top and Bottom) to a specific set of solutions using the DCV's. Using combinatorial analysis, we know without a deep dive that there are a total of 16 potential solutions (2ˆ4, 4 objects with 2 states each, independent of each other), of which we'll want to decide one that is the best to deviate from.
Mapping out solutions
Because the scenarios where Marshmallow enters the top and Donut enters the bottom have opposite solutions, we know the best we can do is a solution that requires at least two DCV's to be moved. We now know there is no optimal solution with only one piece moved or better.
Upon further inspection of solutions, we can see that the bottom right DCV (of the four per solution) prefers to be spun right than left. It's R on three, L on one* (Jellybean has two solutions), and X's for the remaining solutions. This is logically validated because an R on the bottom right DCV protects us from immediate loss by dropping a bottom entering piece directly to the ground. Using the same logic, we also notice that the top left DCV also prefers a Right facing orientation over Left facing. Anchoring the top left DCV and bottom right DCV narrows our search to half of all potential solutions. Not bad!
From here, I simply referenced each potential solution generated from the aforementioned [RX;XR] matrix, to the solutions mapped earlier. By jotting down how many moves we must deviate from these scenarios to solve the 6 different possibilities (remember, we only have to consider the best scenario of Jellybean from Top), we can compare the four constituent solutions generated from the [RX;XR] matrix. Notice this set of solutions validates our earlier determination that we would have no single outcome that would require less than a 2 move deviation.
Now if our definition of best strategy was to solve the most solutions without moving a finger, the [RL;RR] solution (or second to left) produces 4 instant solutions without touching a single DCV. However, this strategy breaks down when a Donut enters the bottom, causing us to move 3 DCV's into the right place, and then another 3 moves to reset. For the same reason the [RR;LR] matrix is also eliminated from being a best strategy for requiring a 3 move deviation. That leaves us with two final Matrices with identical deviation moves, [RL;LR] and [RR;RR] which only require 2 move deviations at worst.
Considering reaction times
Now let's refer back to our solutions matrix, and take a look at how they enter the board to compare which matrix is our best strategy. How can we decide which of the two is more optimal? Since the pieces enter the DCV's in order, we can consider them as ordered solutions. An optimal solution would have the least amount of first-touch DCT moves, as this allows us more reaction time for the user.
For example given the strategy matrix [RL;LR], if a Marshmallow entered the top, I would move the second-touch valve and the third touch valve. Using this logic, we analyze our two finalist strategies from this angle.
Wow! Since a user employing the [RR;RR] matrix strategy would never have to move a first touch DCV, they would always have extra time to react—an advantage that is crucial farther into the game. Because this matrix requires no first touch moves, while [RL;LR] does, I propose this as an optimal solution to Android 404.
You might have noticed that the first default state is a [LL;LL] matrix for a slightly more challenging experience 😉.
Visit Android.com/DavidHirotsu to play (or any other 404 error page on Android.com).